| CSCI203: Algorithms & Data Structures |
Part A:
Question 1
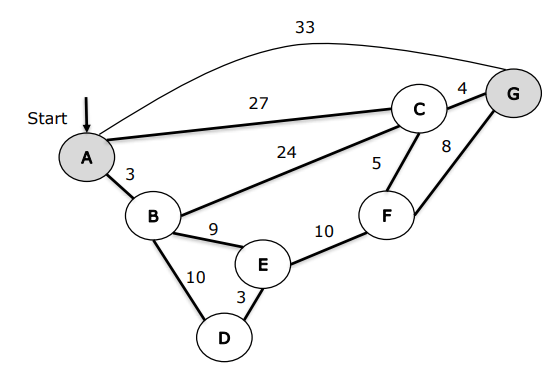
Consider the following network. With the indicated link costs, use Dijkstra’s shortest-path algorithm to compute the shortest path from A to all network nodes.
a) Show how the algorithm works by computing a table like the one discussed in class.
b) Show all the paths from A to all other network nodes.
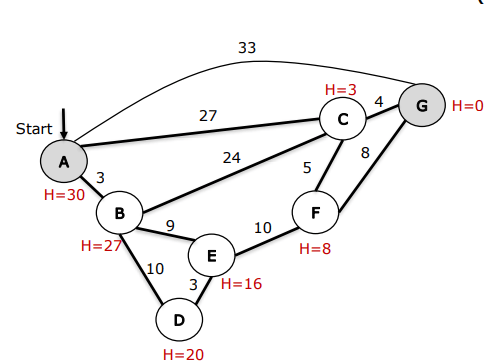
Consider the following search problem, represented as a graph. Each node is a label by a capital letter and the value of a heuristic function is shown in maroon. Each edge is labelled by the cost to traverse that edge. The start state is ‘A’ and the only goal state is ‘G’. Perform the A* search to find the shortest path from node A to node G.
i. Is the heuristics specified in the problem (shown below) admissible? Justify your answer. If the heuristics are admissible, proceed to answer part (ii). If the heuristics are not admissible, correct it with a sensible value of your choice and proceed to answer part (ii).
ii. Perform the A* search to find the shortest path from the start state (S) to the goal state (G).
Part B:
We have discussed greedy algorithms during lectures. A greedy algorithm is an algorithm that recursively constructs a set of objects from the smallest possible constituent parts.
At each one of the iterations, the algorithm takes the best that it can get right now, without regard for future consequences. The algorithm hopes that by choosing a local optimum at each one of the iterations, it can end up at a global optimum.
In this assignment, you will write a program to schedule final examinations for the examination department so that no student has two examinations at the same time.
The goal of this assignment is to expose you to the implementation of greedy algorithms that solves a problem with constraints. You will use a greedy algorithm to determine an assignment of classes to examination slots (schedules) such that:
1. No student, enrolled in two subjects, is assigned to the same examination slot (schedule.)
2. Any attempt to combine two slots into one would violate rule 1. Input to the program will consist of the name of a data file. This file will contain the following data:
The number of students enrolled in the current semester Repeated rows of the following:
- Name of the student and the total number of subjects enrolled
- The subject code the student is enrolled in.
A sample of an input file is as follow: 3
Melissa, 4
CSCI203
CSCI235
CSCI222
CSCI205
Bernard, 4
CSCI213
CSCI222
CSCI204
CSCI203
Terrence, 4
CSCI212
CSCI203
CSCI235
CSCI213
The output of the program should be a list of time slots with the subjects whose final examination will be given at that slot and the total number of students taking the final examination in that slot. One possible output is as follow:
Slot 1: CSCI212, CSCI222 3
Slot 2: CSCI204, CSCI235 3
Slot 3: CSCI205, CSCI213 3
Slot 4: CSCI203 3
The algorithm:
- Read the enrolment information from the input file. As the records are read, build an adjacency matrix representing the relationships among the students and the subject the students enrol in. You should notice that this adjacency matrix is a graph representing the relationships.
Each node of the graph will be a subject taken by at least one student in the current semester. An edge between two nodes will mean there is at least one student taking both subjects. The weight of an edge could be the number of students enrols on both subjects.
- Your aim in solving this problem is to construct a maximal independent set in the graph. This can be achieved by finding an examination schedule satisfying the two constraints mentioned earlier, as follow:
(i) Construct a candidate list of subjects.
(ii) Order the subjects in descending order by a total number of connectivity.
(iii) Starting from the subject with the highest number of connectivity, create a slot.
(iv) Search for a subject to which it is not connected. If you find one, add the subject to the same slot and remove it from the candidate list.
(v) Next, try to find another subject that is not connected to any of those already in the time slot. Similarly, if you find one, add the subject to the same slot and remove it from the candidate list. Continue to do so until
there is no more un-connected subject can be found.
(vi) Accumulate the total number of students enrolled from the adjacency matrix. (How can you do that? Give it a thought.)
(vii) Repeat steps (iii) through (vi) until all the subjects are removed from the candidate list.
- Note that no pair of time slots can be combined without creating a time conflict with a student. Also note that depending on how you select a subject from the candidate list, there may be different schedule can be formed. Any schedule satisfying the two mentioned constrained will be acceptable. You are allowed to implement your algorithm for Part B using C++, Java, or Python.