In Exercise 4.2.27, in finding a confidence interval for the ratio of the variances of two normal distributions, we used a statistic 
which has an Fdistribution when those two variances are equal. If we denote that statistic by F, 
Exercise 4.2.27
Let 
be two independent random samples from the respective normal distributions 
where the four parameters are unknown. To construct a confidence interval for the ratio, 
the variances, form the quotient of the two independent χ2 variables, each divided by its degrees of freedom, namely,
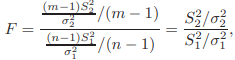
(c) Rewrite the second probability statement as
We caution the reader on the use of this confidence interval. This interval does depend on the normality of the distributions. If the distributions of X and Y are not normal then the true confidence coefficient may be far from the nominal confidence coefficient; see, for example, page 142 of Hettmansperger and McKean (2011) for discussion.